Geometric Brownian Motion Simulation

Geometric Brownian Motion

Geometric Brownian Motion

Here's a simple game:

  1. A fair coin is tossed.
  2. On heads, your wealth increases 50%.
  3. On tails, your wealth decreases 40%.

If you play this game repeatedly many times, your wealth will change randomly. But how, exactly, will it randomly change?

This type of change is called a "random walk", or a "geometric brownian motion". Let's analyze and simulate the game in some different ways.

Analysis and simulations

Enseble average

An average player will gain 5% wealth on each round (each coin toss):
EA = (1.5 + 0.6) / 2 = 1.05

Let's simulate an average player. Here we use 10,000 players (an ensemble) and run the game for 10 rounds. The vertical axis shows average wealth on a log scale:

Time average

If you would participate in the game, you wouldn't be an average player. You would be an individual player and should, on average, loose 5% wealth on each round:
TA = (1.5 * 0.6) / 2 = 0.95

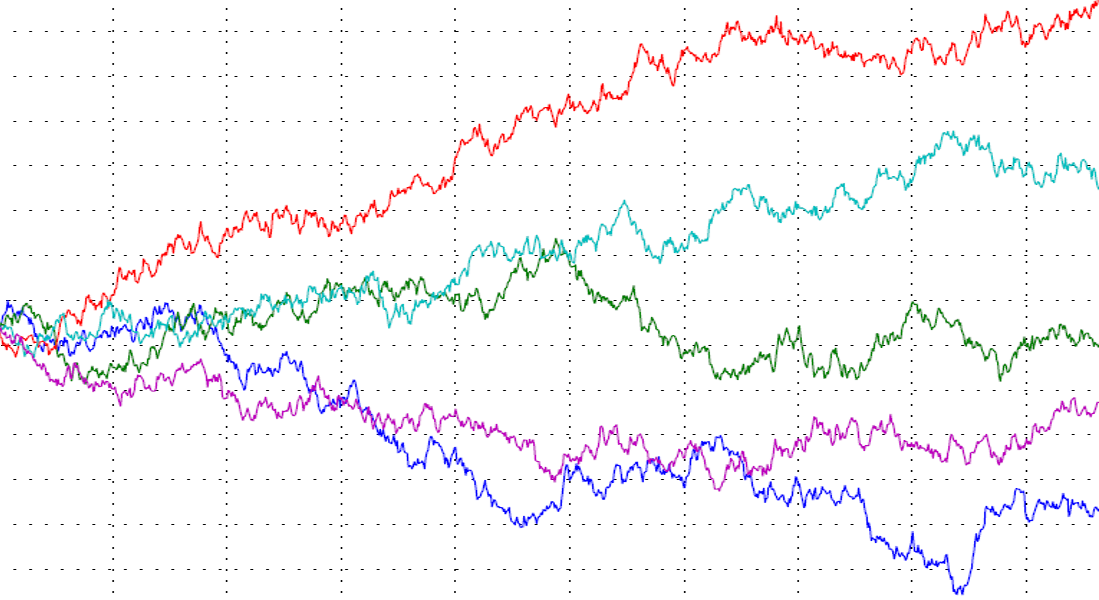
Let's simulatate an individual player. Here we use one single player and run the game 10,000 rounds. The vertical axis shows wealth on a log scale:

Conclusion

Because the ensemble average is not equal to the time average, the game is non-ergodic. The game might seem favourable at first, and for the average player, it is. But for an individual player, the ensemble average is not relevant. It would be irrational to participate.

The Kelly Fraction

Let's slightly modify the game so that a player can choose the amount to bet on each round. In this new scenario, it's in fact possible for an individual player to "get access" to some of the ensemble gains. The optimal amount to bet is calculated by the Kelly Fraction:
KF = P/A - Q/B

P = Probabilty of win
Q = Probability of loss
A = Fraction lost on loss
B = Fraction gained on win

For our game, the Kelly Fraction is:
KF = 0.5/0.4 - 0.5/0.5 = 0.25

Let's run the time average simulation again, but this time using the Kelly Fraction. Here we use a single player making a 25% bet in 10,000 rounds. The vertical axis shows wealth on log scale:

Simulation Code

The simulation code is published here:
https://github.com/ekmwest/gbm-simulation/blob/main/app.js